In 1609, Johannes Kepler (assistant to Tycho Brahe)
published his three laws of orbital motion:
- The orbit of a
planet about the
Sun is an
ellipse with the
Sun at one Focus.
- A line joining a
planet and the
Sun sweeps
out equal areas in equal time.
- The square of the sidereal period of a
planet is directly proportional to the cube of
the semi-major axis of the orbit.
While laws 1 and 2 are statements, law 3 is
presented as an equation:
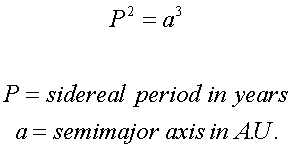
A semi-major axis is the full width of an ellipse.
Law 3 states that if a
planet has a
sidereal orbit
of 11.87 years (like
Jupiter in the previous page),
the diameter of the orbit is:
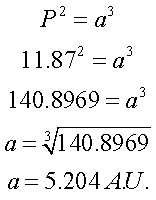
Kepler was not the only one
interested in orbits. Sir Isaac Newton, using his
fundamental work of gravity and forces modified the
Kepler equation to take into account the gravity
effects of the orbiting bodies:

This equation actually gives us a
bit more power. By applying Newton's Law of
Gravitation, we can determine how mass influences
rotation, as well as determine mass if we know the
orbital diameter. To understand this a bit better,
think about the standard forces and centripetal
motions when dealing with an orbit that is circular
(not elliptical like a
planets orbit):

Unfortunately I am not a
mathematics
wizard so I cannot explain the concepts behind these
(and other) equations, but my understanding of these
problems came about by just looking at the equations
(without their corresponding values) and imaging how
each variable interacts with each other. Either way,
hopefully this section (and the other sections) are
helpful.
Back to Top
|

