|
Black Holes: by Alex Nervosa
What is a black hole
and how is it defined?
Theory of
black holes
Formation of black holes
Observations on black holes
Arguments for black holes
Other alternatives…
Relativistic behaviour of black holes
Black holes as power sources
Hawking radiation
Dark matter & the importance of black holes in physics and astronomy
Conclusion
References
Image Credits
Back to
High Mass Stellar Evolution.
What is a black hole
and how is it defined? A black hole is a massive astrophysical object
with infinite density that exerts such a strong gravitational force that nothing
from within its radius can escape, not even light’ (Weisstein 2004). This
General Relativistic definition was defined following the postulation of the
General Theory of Relativity by Albert Einstein in 1915. The term ‘black hole’
was coined in 1968 by physicist John Wheeler and has since been widely accepted
as a description of these peculiar astrophysical objects (Thinkquest 1999).
The existence of mass concentration in ‘dark stars’ however, where their
gravitational force was such that light couldn’t escape from them, was first
postulated in the late 18th century by Reverend John Mitchell and subsequently in
the very late 18th century by Pierre-Simon Laplace (Bunn 1995, Thinkquest 1999).
Both Mitchell and Laplace arrived at the same conclusion using Newton’s theory
of gravitation using the notion that light behaved as a particle.
Back to Top |
Back to
High Mass Stellar Evolution
Theory of
black holes The General Relativity describes a set of field equations that
describe the properties and behavior of gravity surrounding a given mass. In
other words the field equations describe how an object curves space-time and how
the curvature in turn, alters mass in three dimensional space (Smarr 1995) The
first person to apply General Relativity’s field equations in relation to
stellar objects was German physicist Karl Schwarzschild in the year 1916. Using
Einstein’s field equations, Schwarzschild found for a mass concentrated inside a
critical radius, which is defined as the distance from the centre of the mass,
no object within this radius can pass to the outside, not even light. This
definition is known as the Schwarzschild radius (Freedman & Kaufmann 2002), and
is also the definition of the critical radius referred to earlier in the
introduction. The calculation of the Schwarzschild radius has only a single
variable that affects it, which is the object’s mass (Hamilton 1999). This was
an important first step in providing a quantitative description of a black hole.
It was important also in implicitly defining another structural property of a
black hole called the ‘event horizon’. The event horizon is a region
surrounding a black hole where light cannot escape, yet cannot be drawn inside
the black hole. The event horizon is located at the Schwarzschild radial
distance from the centre of a black hole. Light rays at the event horizon trace
a circular path around a black hole. As a consequence the event horizon forms a
‘virtual’ surface around a black hole which is governed by the length of the
Schwarzschild radius. The event horizon and the Schwarzschild radius together
mark the virtual boundary of no return for objects that come within this area of
a black hole. The structural properties of a black hole, as described by the
Schwarzschild radius and the event horizon were further extended in 1965 by
Roger Penrose, who proved the Singularity Theorem (Weisstein 2004). Penrose, a
professor in mathematics, was able to derive this theorem by using, at the time,
a new mathematical tool which hadn’t previously been used in general
relativistic calculations, called Topology (Thorne 1994). The singularity
theorem states that inside every black hole, there is a point or location of
infinite density called a singularity. Any object which moves within the
Schwarzschild radius is inexorably drawn towards the singularity until it is
ultimately destroyed. A singularity is a point or place of infinite density.
It can either be located at the centre of a non-spinning black hole as a point
of infinite density or around the centre of a spinning black hole as an
infinitely thin ring. The characteristics of the singularity depend on
characteristics inherited by a black hole during formation, such as whether it
has angular momentum or not. These characteristics also affect the structure
of a black hole such as the length of the Schwarzschild radius which is the
distance of the event horizon from the singularity (Freedman & Kauffman 2002).
The characteristics are simply: Mass, angular momentum and electric charge (Gundlach
1999). They form the essence of the No Hair Theorem of black holes postulated by
John Wheeler in 1967 (Novikov 1990). The implications of the No Hair theorem are
that only mass, angular momentum and electric charge are required to completely
describe a black hole. During black hole formation, attributes which are
spherical protrusions of a stellar object are gravitationally radiated away, for
instance the magnetic field. This behaviour described as ‘gravitating away’
characteristics during black hole formation was postulated by Richard Price in
Price’s theorem in the year 1970 as described by Weisstein (2004). Price’s
theorem explains why certain information about a stellar object is lost during
black hole formation and also helps to understand why so few characteristics
described by the No Hair Theorem, namely mass, angular momentum and electric
charge are required to completely describe and determine the structure of a
black hole. Characteristics and structural properties of a black hole although
very few, can be combined and described in the following solutions to General
Relativity’s field equations (Schwarzschild, Reissner-Nordstrom, Kerr and
Kerr-Newman), as follows:

Table 1: Properties of black holes
Points to note:
- The ergoregion is a region of space-time located outside the event
horizon of a rotating black hole where no object even if traveling at the
speed of light, can remain stationary. Unlike the event horizon, the
ergoregion is a physical concept. It is bounded between a ‘static limit’
which is the outer rim of the ergoregion and the event horizon (see Figure
1) which also marks the inner rim of the ergoregion. An object can enter and
exit the ergosphere from the static limit, however once the static limit is
entered an object will start to be drawn towards the black hole.
- The ergoregion* and shape** of a black hole are attributes derived by
existence of or absence of angular momentum i.e. Schwarzschild and
Reissner-Nordstron black holes are circular and don’t have an ergoregion,
whilst Kerr and Kerr-Newman black holes are oblate spheroids and have an
ergoregion. Angular momentum also defines whether or not a point singularity
(for a non rotating black hole) or ring singularity (for a rotating black
hole) exists.
Figure 1: Kerr-Newman Black Hole:
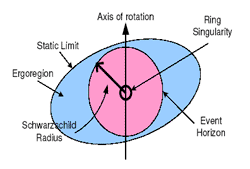 |
The Kerr-Newman black hole shown on the left is characteristic
of structure and properties attributed to a spinning black
hole.
The entire mass of a black hole is located in the singularity
(shown as a black ‘ring’ in Figure 1).
The single most important characteristic of a black hole
responsible for governing everything about its’ formation, structure
and evolvement, is its mass; More specifically, the inherited mass
of the compact object before black hole formation for example, a
collapsing star under its own self gravity. |
There is however, a theoretical mass limit called the ‘Chandrasekhar
limit’ (Darling 2003) that defines the maximum mass a degenerate (Hyperphysics
2004) compact stellar object may have. The Chandrasekhar limit for nuclear
degeneracy, after which black hole formation may be possible has been
calculated at approximately 3 solar masses (ThinkQuest 1999, Freedman &
Kaufmann 2002). If the Chandrasekhar limit is exceeded, the stellar
object’s degenerate nuclear pressure which normally acts to stop further
compression under self gravity will not be able to halt its own
self-implosion. At this point, General Relativity effects become prevalent
as gravity begins to dominate over the degenerate pressure, forcing a black
hole to form.
Back to Top |
Back to
High Mass Stellar Evolution
Formation of black holes There are a number of ways
in which a black hole can form: Collapse of a compact stellar remnant,
accretion of matter in a compact stellar remnant, merger of compact stellar
remnants and gravitational collapse of dense regions of matter in the
Universe responsible for super massive black hole formation.
Figure 2: Stellar Collapse:
 |
The collapse of stellar remnants, also known as ‘core collapse’
after a supernova explosion (Figure 2), occurs when the
Chandrasekhar limit for nuclear degeneracy is exceeded for a massive
stellar object of more than 20 solar masses (Fryer 1999). The
implication of this are that, only large massive stellar objects are
capable of forming stellar black holes after their degenerate core
collapses. |
There are however, other ways in which black holes may form even when
stellar masses are less than 20 solar masses. It can occur in accretion of
matter around degenerate compact stellar remnants such as white dwarfs or
neutron stars that typically have a degenerate mass less than the
Chandrasekhar limit (Freedman & Kaufmann 2002).
Figure 3: Accretion in a Binary System:
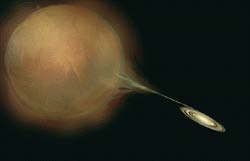 |
If for instance, a white dwarf or neutron star exists in a
binary system with a stellar companion such as a stellar giant or
supergiant, matter lost from the companion star, either ejected via
strong stellar winds or ejected from the companion star via inner
Lagrangian overflow of its Roche lobe (Audley 1998) as depicted in
Figure 3, can accrete either on a white dwarf or neutron star, to
the point where the Chandrasekhar limit is exceeded, causing General
Relativity effects to take over, resulting in black hole formation. |
Figure 4: Merger of Compact Stellar Remnants:
 |
The merger of compact stellar remnants, for example a binary
system composed of two neutron stars orbiting each other, each
creating their own spacetime curvature as shown in Figure 4, is
another possible path to black hole formation. If the two neutron
stars merged as a result of orbit in-spiralling due to General
Relativistic effects associated with gravitational wave emission
(Seidel 1995), the combined mass which will result from the merger
will exceed the Chandrasekhar limit. At this point black hole
formation will take place. |
Figure 5: Super Massive Black Holes:
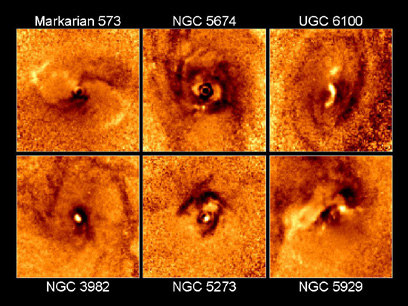 |
To date, galactic centers observed to have bulges, appear to
host super massive black holes. These super massive black holes are
very large and are of the order of up to billions of solar masses
(Britt 2003). One of the most prevalent theories used to explain
super massive black hole formation cites gravitational collapse
during early galactic formation in the dense centre of galaxies. It
is thought that super massive black hole formation at the centre of
galaxies is responsible for influencing galactic evolution and
galactic structure (Kormendy & Shields 2000). Figure 5 shows Hubble
space telescope images taken in visible and near-infrared
frequencies of active galactic centers thought to be the location of
super massive black holes.
There are other potential ways in which black holes may or may
have formed: It is theorized that ‘primordial’ black holes may have
formed in the early Universe where the density contrast was high
enough to allow matter to coalesce under its own self gravity (Boudoul
& Barrau 2002). |
As a consequence primordial black holes could be of various masses,
depending on the magnitude and variance of the density contrast of early
regions of the Universe where formation of these primordial black holes may
have taken place. To date, no primordial black holes have been observed,
although it may be possible to detect these via thermodynamical effects
occurring outside their event horizon (Rankin 1995) if ever these effects
could be measured.
It is theorised also, that ‘quantum’ black holes can form however, it is
suggested that these may only exist in higher dimensions that we cannot
readily observe (Kaku 1998). Quantum black holes would appear to be
infinitesimally small with a Schwarzschild radius approximately that of an
atomic nucleus (Rabinowitz 1999). It has been suggested by Giddings (2001)
and Thomas and Giddings (2002), that these quantum black holes could
possibly be created in the next generation of high energy particle
accelerators currently being developed in Europe.
Back to Top |
Back to
High Mass Stellar Evolution
Observations on black holes
Although there are various theories on formation of black holes from an
observational perspective, there are only two classifications astronomers
make for them based on mass, which are stellar and super massive black
holes.
Stellar black holes generally have a mass above 20 solar masses, however,
it is not uncommon for them to possess as low as 3 solar masses (Freedman &
Kaufmann 2002). Stellar black holes which have between 100 and 500 solar
masses, usually called ‘mid-mass’ black holes have also been found, however
these are less common than their less massive counter parts (Fazekas 2004).
Figure 6: Halo Black Hole Candidate:
 |
Stellar black holes are likely to be found in many places of the
observable Universe. Galactic halos for instance can host ‘halo’
black holes, which are usually found as individual stellar black
holes as described by Phillips (2000) with the discovery of
MACHO-96-BLG-5 black hole candidate as an example shown in Figure 6.
More commonly, stellar black holes may be found as part of X-ray
binary systems either in globular clusters or in the vicinity of
galactic centers or galactic spiral arms, where they are accompanied
by their respective stellar companion for example a stellar giant or
low mass main sequence star. |
Figure 7: X-ray Binary system:
 |
V404 Cygni in the constellation Cygnus is an example of an X-ray
binary system containing a black hole accompanied by a K0 III
stellar giant (Mendez 2003). An artist’s impression in Figure 7
depicts V404 Cygni siphoning off matter from its companion star onto
its accretion disk thus emitting X-rays from matter outside the
event horizon.
Stellar X-ray binary system black holes are interesting
astronomical objects as the accretion disk and the orbiting
companion as depicted in Figure 7 can be used to determine
structural and associated black hole characteristics.
|
With careful observations of X-ray binary systems, important information
such as mass, angular momentum, semi-major axis and orbital period of a
stellar black hole can be inferred.
Masses of stellar black holes are arguably the most important
characteristic that may be indirectly inferred. When mass is inferred,
distinctions can be made between stellar black holes and other potential
compact stellar remnant candidates such as neutron stars and white dwarfs,
both of which may be found in X-ray binary systems also. Observations of
mass and other characteristics of stellar black holes found in the galactic
halo, or halo black holes, are more difficult to make as they don’t have an
orbiting companion that can assist in determining their inferred properties.
Some indirect observational methods and techniques used for stellar black
holes are:
- Spectral analysis of a black hole’s X-ray accretion disk. This can
be used to infer a black hole’s mass as the luminosity associated with
the inner accretion disk around a black hole is related to the mass of
the black hole (Fazekas 2004). Also analysis of X-ray emission from the
disk’s iron atoms can indicate how rapidly or otherwise a black hole is
spinning (Watzke 2003).
- Usage of Kepler’s 3rd law and Newton’s form of Kepler’s third law
combined with CCD photometry, spectroscopic, Doppler, radial velocity
and light curve analysis of accretion disks and/or companion stars in
X-ray binary systems. These techniques combined in various forms can
determine a stellar black hole’s mass, rotational period and semi-major
axis (Freedman & Kaufmann 2002).
- Measuring spectroscopic gravitational red shift in an X-ray binary
system. This can be used to infer the mass of a stellar black hole and
draw distinctions between types of X-ray binary systems i.e. those which
contain stellar black holes and those that do not (Reynolds & Nowak
2003).
- Resonances between Quasi Periodic Oscillations (QPOs) and
orbital/circular motions of accreting matter in an X-ray accreting disk,
can be used to determine the angular momentum of a stellar black hole (Abramowicz
& Kluzniak 2001).
- Gravitational micro lensing of halo black holes can be used to
determine their mass, which is inferred as a result of the duration of
the lensing event detected. This event is the time duration of the
apparent brightness usually detected by orbiting or Earth based
telescopes (Phillips 2000).
Uncertainties associated with stellar black hole measurements can be a
problem. Mass uncertainties for high mass X-ray binaries which are black
holes accompanied by a high mass stellar companion, are higher than those
for low mass X-ray binaries which are for black holes accompanied by a low
mass stellar companion, as described by Hughes (1999) and Silber (1999). The
gravitation field in a high mass X-ray binary system resulting from a black
hole’s orbiting companion will be greater, thus affecting the accuracy of
spectroscopic measurements obtained of a stellar black hole’s accretion
disk.
Gravitational lensing techniques are not entirely accurate. Halo black
hole masses therefore have a high level of uncertainty as describe by Hughes
and Holz (2003). One of the reasons is that there are uncertainties in
deriving and determining lensing parameters used to obtain results however,
as described by Han (1997), work in this area is continuing to improve the
accuracy of lensing measurements.
A super massive black hole’s mass and angular momentum can be inferred
using the same methods and techniques described for stellar X-ray binary
systems, as super massive black holes and stellar X-ray binary system black
holes share the same characteristics e.g. orbiting companions such as other
stars and gas clouds as well as accreting disks outside their event horizon.
Super massive black holes are located in the centre of bulging galaxies and
have been found to contain masses in the order of millions to billions of
solar masses (Lochner 2004).
The closest example of a super massive black hole is Sagittarius A*
(abbreviated to Sgr A*) which is located at the centre of our Milky Way
galaxy (Weinstock 2000). There have been several observations conducted of
Sgr A* over a variety of wavelengths to attempt to confirm its status as a
super massive black hole, as well as to determine it characteristics and
attributes such as mass and angular momentum.
Sgr A* has been found to emit electromagnetic radiation primarily in the
radio frequency region and also more recently, as observed by the Chandra
X-Ray observatory in the X-ray region (Tucker 2000). These observations
along with infrared imaging performed by the Hubble space telescope have
enabled according to Watson (2001), astronomers to detect the following
insofar as Sgr A*:
- Doppler shifts of surrounding gas clouds
- Doppler shifts of surrounding stellar objects
- The proper motion of surrounding stars, over time
- The mass distribution around the central region of our galaxy
The Hubble telescope image shown in Figure 8 of Sgr A* indicated by
yellow arrows shows stars surrounding Sgr A*, most of which have had their
Doppler shifts and proper motion measured using some of the observation
described above. Although not shown in this picture, the majority of stars
depicted have been observed to be orbiting either clockwise or anticlockwise
around Sgr A*. Results of the above observations described by Watson (2001)
constrained mass and associated properties of Sgr A*’s and have verified its
status as a super massive black hole (Ghez et. al. 2003).
Figure 8: Sgr A* and Orbiting Stars:
 |
More recent results by Falcke (2004) and his team of
astronomers, using very long baseline interferometry (VLBI) (Goebel
et. al 2004) have determined precisely the size of Sgr A* by using
high frequency VLBI techniques in the radio frequency spectrum
better known as millimeter VLBI. Millimeter VLBI is optimal for
piercing through the intervening interstellar dust found towards the
centre of our galaxy. Falcke and his team found the size of Sgr A*
to be 2 astronomical units in diameter which is equivalent to the
diameter of the Earth’s orbit around the Sun. |
Back to Top |
Back to
High Mass Stellar Evolution
Arguments for black holes
Arguments for black holes, other than those based on the fact that they
don’t inherently emit any light, can be made based on inferred mass
observations of potential black hole candidates. As described earlier, the
Chandrasekhar limit for nuclear degeneracy is around 3 solar masses. Suspect
black holes where the inferred mass is greater than this limit may be
described as a black hole candidate.
Supportive arguments in addition to those around a greater-than
Chandrasekhar limit can also be made based on gravitationally red shifted
spectrum from the accretion
disk in an X-ray binary system. A black hole candidate for instance will
exert more gravitational force, hence gravitational red shift on light
emitted from its accretion disk. The spectrum detected will show specific
features not found from spectra of other compact stellar objects such as
quark, neutron stars and white dwarfs, such as the “broad iron K-line”
effect (Reynolds 1997, Britt 2002).
Additional arguments for black holes can also be made based on the
absence of Type I X-ray bursts from black holes which are commonly found in
neutron stars as a consequence of thermonuclear explosions on their surface
crust. The absence of Type I X-ray bursts may therefore serve as indirect
confirmation of the existence of the event horizon, thus inferring the
existence of black hole (Narayan 2002).
Back to Top |
Back to
High Mass Stellar Evolution
Other alternatives…
There are other more recent theoretical solutions to Einstein’s General
Relativity field equations that may be used as alternatives that may explain
the behavior of low mass stellar black holes. “Q-stars” are one of those,
also known as ‘strange’ or ‘quark’ stars as described by (Miller Shahbaz
Nolan 1998; Gondek-Rosinska Kluzniak Stergioulas 2002). Q-stars are another
class of compact stellar objects with a mass above the Chandrasekhar limit
for nuclear density, up to 10 solar masses (Abramowicz Kluzniak & Lasota
2002).
Another theoretical solution to Einstein’s General Relativity field
equations are gravitational vacuum stars also known as “gravastars” (Visser
& Wiltshire 2004). Gravastars are condensations of atomic matter at
extremely low temperatures which are enveloped in a thick membrane akin to a
surface crust (Britt 2002). A gravastar’s structure is different to a black
hole, as no event horizon or singularity exists however it would be
difficult to distinguish a gravastar from a black hole as its’ membrane
would be at a distance from its’ centre just greater than the Schwarzschild
radius, hence having similar dimensions to a black hole. A gravastar’s
behavior would be indistinguishable to a black hole insofar as space-time
warping effects and in having an accretion disk in stellar X-ray binary
system (Mazur & Mottola 2001, Abramowicz Kluzniak & Lasota 2002). To date,
no direct or indirect observations have been made of Q-stars or gravastars.
Back to Top |
Back to
High Mass Stellar Evolution
Relativistic behavior of black holes
Black holes as a result of their strong gravitational force are able to
accelerate particles such as protons and electrons to relativistic speeds
(speeds approaching the speed of light) outside their event horizon (Grenier
& Laurent 2001).
This behavior is observed in stellar X-ray binary black holes and super
massive black holes both which are depicted in Figure 9. An example already
familiar is that of X-ray emission from an accretion disk outside a black
hole’s event horizon. Electrons and protons spiraling towards a black hole
in an accretion disk are accelerated to relativistic speeds resulting from
conservation of angular momentum as they approach the event horizon.
Friction results between the particles, which produce high energy X-rays
from the accretion disk (Hughes 1999).
A notable difference between the accreting disk of a super massive black
hole and a stellar X-ray binary black hole is the larger disk size of super
massive black hole described by Daunt & Yost (2001) also depicted in Figure
9. X-ray emissions generally occur in bursts resulting from fluctuations in
accretion volumes of matter outside the event horizon. This effect is
observed in Soft X-Ray Transients (SXT’s for short) which are a type of
stellar X-ray binary system described by Narayan (2002). The already
familiar V404 Cygni is an example of an SXT.
Figure 9: Accretion Disks and Relativistic Jets:
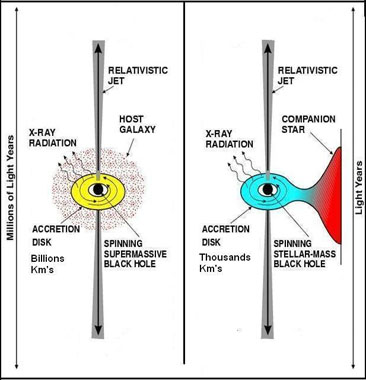 |
Detection of X-ray fluctuations can be detected by CCD X-ray
cameras and transmission grating X-ray spectrometry via orbiting
X-ray detection satellites such as NASA’s Chandra X-ray observatory
and Japan’ ASCA X-ray detection satellite (Bradt et al 2001).
Relativistic behavior of black holes is also observed from emission
of relativistic jets resulting from synchrotron radiation outside a
black hole’s event horizon as depicted in Figure 9. These collimated
jets of synchrotron radiation result primarily from plasma composed
of protons, electrons and positrons. The end points of each jet are
characterized by radio frequency emission. Stellar X-ray binaries
which have black holes and radio emissions resulting from
relativistic jets are sometimes referred to as to as microquasars or
radio-jet X-ray binaries (Farlex Inc. 2004) to distinguish them from
other stellar X-ray binaries. Jets emitted from microquasars span
over a distance of light years as shown in Figure 9. |
Super massive black holes also exhibit the same characteristics as
microquasars, however they have jets which span over millions of light years
as depicted in Figure 9. Microquasars are extremely useful in comparative
studies of quasars which harbor super massive black holes that possess the
same relativistic behavior as microquasars. These studies allows structural
comparisons between both to be performed and behavioral predictions of
quasars to be made such as their relativistic behavior, given that time
events in microquasars occur over much shorter time scale than for quasars
e.g. days instead of centuries (Mirabel 2002).
Back to Top |
Back to
High Mass Stellar Evolution
Black holes as power sources
Figure 10: Quasars Are Found In AGN’s:
 |
AGN’s Super massive black holes have varying power producing
abilities governed by:
- 1. Their inherent mass and
- The amount of matter available around them typically drawn
on their accretion disks (Lochner 2003).
Quasars, which are the most intense sources of energy know in the
Universe, harbor at their core super massive black holes (SDSS
2002). Active galactic nuclei (AGN’s for short), which form part of
the core of bulging ‘active galaxies’ (depicted as the second object
from the top in Figure 10), harbour super massive black holes
responsible for their power source also. |
The first object from the top in Figure 10 shows another type of bulging
galaxy labeled ‘normal spiral galaxy’ which also harbors a super massive
black hole. These ‘Normal spiral galaxies’ better known as ‘radio galaxies’
have a relatively less energetic galactic nucleus, as a consequence of less
energy produced by their respective super massive black hole also located at
their centre (Weiss 2004).
Back to Top |
Back to
High Mass Stellar Evolution
Hawking radiation
Arguably the most peculiar behavior that a black hole possesses is its
ability to radiate energy and through this process lose mass in a process
called ‘Hawking radiation’, named after the contemporary theoretical
astrophysicist Stephen Hawking (Hamilton 1998).
To understand how Hawking radiation works, one needs to consider that,
what we describe as the ‘vacuum’ of space is in fact not a vacuum at all.
The Heisenberg uncertainty principle (Freedman & Kaufmann 2002) being one of
the key tenets of quantum physics allows for the existence of virtual
particles in the vacuum of space. These virtual particles are extremely
short lived. They cannot be detected. They annihilate each other in pairs as
soon as they are created given each has opposite electric charges. What we
observe though is the end result of their annihilation, such as ‘real’
particles created for example photons, electrons and positrons.
In the vicinity of the event horizon, it is possible that the extremely
strong gravitational force induced on virtual particle pairs is able to draw
one of the particles with negative energy from the pair inside the event
horizon, thus, forsaking it forever (see left part of figure 11). As a
consequence the remaining positive energy virtual particle has no choice but
to become a real particle. It must do so in order not to violate the
Heisenberg uncertainty principle. However it cannot do so without its
partner.
Figure 11: Virtual Particles:
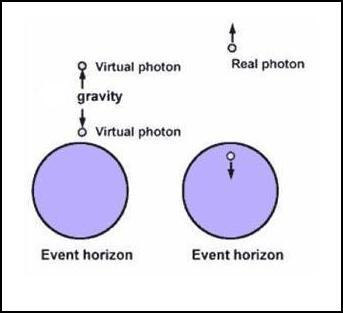 |
In order then, for the orphaned virtual particle to become a
real particle some of the energy of the black hole’s gravity must be
converted to matter. This apparent loss of gravitational energy is
equivalent to mass being lost from inside the black hole. Mass lost
from inside a black hole can also be described in terms of ‘quantum
tunneling effects’ described by Lochner (2003). The end result is
that: 1) energy is radiated away outside the black hole’s event
horizon and 2) Although it appears that energy is ‘lost’ from
conversion of mass into gravitational energy, the net effect is that
energy is conserved as the gain in ‘positive’ energy emitted outside
the event horizon is equally compensated by the gain of ‘negative’
energy by the black hole.
The implication of this for black holes is that they thermally
radiate over a range of wavelengths in a similar way to ordinary
stars i.e. temperature is associated with black holes. |
Hawking’s radiation theory of black holes also finds that the energy lost
from a black hole is inversely proportional to its mass. Larger mass black
holes have low temperatures and therefore don’t radiate much energy. They
also radiate at low frequencies e.g. radio or microwave frequencies. Smaller
mass black holes emit more energy, hence have higher temperatures and higher
frequency for their energy emission e.g. X-rays and gamma rays (Thinkquest
2000) are produced. Finally, the subsequent implication of the inverse
thermal/mass relationship is that black holes will suffer from thermal
radiation runaway effects as their mass gets smaller towards the end of
their life, meaning that they will lose mass faster, the smaller they
become.
Hawking radiation has implications for the existence or lack thereof of
primordial quantum black holes. If primordial quantum black holes existed
early in the history of the Universe it is very likely that some of these,
being extremely small, would have radiated away (Schomberg 2002) via Hawking
radiation.
Mass loss, hence energy loss due to Hawking radiation, which in turn
raises a black hole’s temperature, occurs very, very slowly over a long
period of time. It would take 1E+60 years for a black hole of 5 solar masses
or 1E+80 years for a super massive black hole of 5 million solar masses as
an example, to evaporate via Hawking radiation (Freedman & Kaufmann 2002).
This greatly exceeds the estimated age of the Universe, which is currently
estimated to be 1.5E+10 years.
It is important to note that the ratio of Hawking radiation luminosity
emitted, versus a black hole’s disk accretion luminosity, over the course of
its life, is extremely small even after taking into consideration that both
Hawking radiation luminosity and disk accretion luminosities change over the
lifetime of a black hole (Graham 2003; Thinkquest 2000; Sekmen 2003).
Back to Top |
Back to
High Mass Stellar Evolution
Dark matter & the importance of black holes in physics and astronomy
One of the most baffling mysteries in modern astronomy is that 80% to 90%
of matter in the observable Universe required to explain its composition and
structure is ‘dark’ matter which is unseen and unaccounted for i.e. it is
missing (Smith 1999).
There are a number of theories that individually attempt to account for
dark matter, detailed by Russell & Halls (1999), which include the existence
of black holes and red dwarfs1 or tau neutrinos2
amongst many others. However Russell & Halls as well as Delehunty (2004)
conclude that these theories alone or collectively, cannot all account for
this missing matter. This view is shared by a number of astronomers and
astrophysicists hence the hunt currently continues to understand what dark
matter is.
Consequentially, black holes are just one possibility that may account
for some of the dark matter of the Universe and not the only one. Primordial
black holes are one possibility which may account for dark matter, as
conditions in the early Universe being far more dense than today, would have
favored gravitational collapse of entire regions of space-time potentially
creating primordial black holes of varying masses (Boudoul & Barrau 2002).
Another black hole candidate that may contribute to dark matter is the
‘halo’ black hole described earlier. There may be many, many more halo black
holes in the Universe than we can currently account for (Martin 1996) as
they are difficult to observe indirectly given gravitational lensing
techniques currently best suited for their observation, are still being
perfected (Han 1997).
Black hole research is extremely important for physics and astronomy as
it serves to validate General Relativity postulates as well as contribute to
the formulation of the Theory of Quantum Gravity which provides a link
between Quantum Physics and General Relativity being one of the main goal of
modern physics and astronomy.
Further research into black holes will assist also to understand the
extent that they play in dark matter which is also one of the most important
goals of modern astronomy.
______________________________________________________________________________________________
1 Black holes and red dwarfs belong to the MACHO (MAssive
Compact Halo Object) class of objects, which are localized to the Galactic
Halo
2 Tau neutrinos belong to the WIMP (Weakly Interacting Massive
Particles) class of objects which are particles that don’t interact with
baryonic matter (baryonic matter includes particles such as protons and
neutrons)
______________________________________________________________________________________________
Back to Top |
Back to
High Mass Stellar Evolution Conclusion Black holes are compact massive objects with infinite
density that have the ability to warp the space-time curvature and in doing
so ensure that nothing, not even light can escape from them. Their structure
although having only a few attributes, allows various characteristics to be
associated with them such as spin and electric charge. They can be
categorized by mass as either stellar or super massive black holes and they
form under a variety of circumstances generally associated with
gravitational attraction or gravitational collapse of matter. The indirect
observational techniques used for stellar and super massive black holes are
generally the same. Although there are uncertainties in observational
results there is enough evidence to support the presence of black holes over
other compact stellar remnants, however there are also other alternatives to
black holes as described by more recent solutions to General Relativity
field equations that deserve consideration. Black holes exhibit
relativistic behavior; Examples covered were X-ray emission from accretion
disks and relativistic jets, which are features also found at the heart of
quasars and active galactic nuclei (AGN) where super massive black holes
play a major role as ‘power sources’ to these phenomena. Black holes have a
theoretical finite lifetime resulting from Hawking radiation that associates
a thermal temperature and mass evaporation effect to these intriguing
objects. We have also seen how black holes contribute to the unseen dark
matter in our Universe and the importance that the theoretical and
observational work around them plays in modern physics and astronomy.
Back to Top |
Back to
High Mass Stellar Evolution
References: Abramowicz M. A., Kluzniak W., 2001, A Precise Determination
Of Black Hole Angular Momentum In GRO J1655-40,
http://au.arxiv.org/abs/astro-ph/0105077 Abramowicz M. A., Kluzniak
W., Lasota J. P., 2002, No Observational Proof Of The Black-Hole
Event-Horizon,
http://au.arxiv.org/abs/astro-ph/0207270 Audley D., 1998, Mass
Transfer,
http://lheawww.gsfc.nasa.gov/users/audley/diss/node8.html Boudoul G.,
Barrau A., 2002, Some Aspects Of Primordial Black Hole Physics,
http://au.arxiv.org/abs/astro-ph/0212225 Bradt H., Canizares C.,
Chakrabarty D., Clark G., Lewin W., Rappaport S., 2001, Astrophysics: X-ray
Astronomy,
http://web.mit.edu/physics/research/areasofresearch/astrophysics/x-ray_astronomy.html
Britt R. R., 2002, The Great Escape,
http://www.space.com/scienceastronomy/astronomy/blackhole_light_020626.html
Britt R. R., 2002, Thick Skinned Gravastars Vie To Replace Black Holes – In
Theory,
http://www.space.com/scienceastronomy/astronomy/gravastars_020423.html
Britt R. R., 2003, The New History Of Black Holes,
http://www.space.com/scienceastronomy/blackhole_history_030128-1.html
Bunn T., 1995, Black Holes FAQ,
http://cosmology.berkeley.edu/Education/BHfaq.html Darling D, 2003,
The Encyclopaedia Of Astrobiology, Space And Flight,
http://www.daviddarling.info/encyclopedia/C/ChanLimit.html Darling D,
2003, The Encyclopaedia Of Astrobiology, Space And Flight,
http://www.daviddarling.info/encyclopedia/C/ChanLimit.html Delehunty
M., 2004, Space Science Section – Dark Matter,
http://www.astronomytoday.com/cosmology/darkmatter.html Falcke H.,
2004, The Black Hole In The Galactic Centre,
http://www.mpifr-bonn.mpg.de/staff/hfalcke Farlex Inc., 2004,
Microquasars,
http://encyclopedia.thefreedictionary.com/Microquasar
Fazekas A. S., 2004, Mounting Evidence For Middleweight Black Holes,
http://www.astronomy.com/Content/Dynamic/Articles/000/000/001/265locve.asp
Freedman R. A., Kaufmann W. J., 2002, Universe Fryer C. L., 1999, Mass
Limits For Black Hole Formation,
http://arxiv.org/abs/astro-ph/9902315
Ghez A. M., Salim S., Hornstein S. D., Tanner A., Morris M., Becklin E.
E., Duchene G., 2003, Stellar Orbits Around The Galactic Center Black Hole,
http://au.arxiv.org/abs/astro-ph/0306130
Giddings S. B., 2001, Black Hole Production In TeV-scale Gravity, And The
Future Of High Energy Physics,
http://www.arxiv.org/abs/hep-ph/0110127
Grenier I. A., Laurent P., 2001, X-ray And Gamma-ray Astronomy,
http://www.europhysicsnews.com/full/12/article6/article6.html
Goebel G. et. al., 2004, Radio Astronomy,
http://kosmoi.com/Science/Astronomy/Radio/
Gondek-Rosinska D., Kluzniak W., Stergioulas N., 2002, An Unusually Low
Mass Of Some “Neutron” Stars?,
http://arxiv.org/pdf/astro-ph/0206470
Graham J. R., 2003, Disk Luminosity And Accretion Rates,
http://astron.berkeley.edu/~jrg/ay202/node116.html Gundlach C., 1999,
Black Hole Charge And Angular Momentum,
http://relativity.livingreviews.org/Articles/lrr-1999-4/node19.html
Hamilton A., 1998, Hawking Radiation,
http://casa.colorado.edu/~ajsh/hawk.html
Hamilton A., 1999, More About The Schwarzschild Radius,
http://casa.colorado.edu/~ajsh/schwp.html
Han C., 1997, Correction For Blending Problem In Gravitational
Microlensing Events,
http://arxiv.org/abs/astro-ph/9704212
Hughes A., 1999, The Strangest Remnant Of Them All (Swinburne University
Of Technology – Swinburne Astronomy Online HET603)
Hughes A., 1999, Black Holes (Swinburne University Of Technology –
Swinburne Astronomy Online HET603)
Hughes S. A., Holz D. E., 2003, Cosmology With Coalescing Massive Black
Holes,
http://www.iop.org/EJ/abstract/0264-9381/20/10/308 Hyperphysics, 2004,
Neutron Degeneracy,
http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.html
Kaku M., 1998, Black Holes, Worm Holes And The 10th Dimension,
http://home.flash.net/~csmith0/black.htm
Kormendy J., Shields G., 2000, Monsters In Galactic Nuclei,
http://chandra.as.utexas.edu/~kormendy/stardate.html
Lochner J., 2003, More On Hawking Radiation,
http://imagine.gsfc.nasa.gov/docs/ask_astro/answers/011125b.html
Lochner J., 2004, Active Galaxies And Quasars,
http://imagine.gsfc.nasa.gov/docs/science/know_l1/active_galaxies.html
Martin D., 1996, Dark Matter Investigation,
http://aci.mta.ca/TheUmbrella/Physics/P3401/Investigations/MassGalaxyDM.html
Mazur P. O., Mottola E., 2002, Gravitational Condensate Stars: An
Alternative To Black Holes,
http://au.arxiv.org/abs/gr-qc/0109035
Mendez J., 2003, ING Scientific Highlights In 1992,
http://www.ing.iac.es/PR/SH/SH92/high_92.html
Miller, Shahbaz, Nolan, 1998, Are Q-Stars A Serious Threat For
Stellar-Mass Black Hole Candidates?,
http://www.blackwell-synergy.com/links/doi/10.1046/j.1365-8711.1998.01384.x/abs
Mirabel I. F., 2002, Microquasars As Sources Of High Energy Phenomena,
http://nedwww.ipac.caltech.edu/level5/Sept02/Mirabel/Mirabel1.html
Narayan R., 2002, Evidence For The Black Hole Event Horizon,
http://www.blackwell-synergy.com/links/doi/10.1046/j.1468-4004.2003.44622.x/full
Novikov I., 1990, Black Holes and the Universe Phillips T., 2000, Black
Holes On The Loose,
http://www.southpole.com/headlines/y2000/ast14jan_1.htm
Rabinowitz M., 1999, Little Black Holes, Dark Matter And Ball Lightning,
http://au.arxiv.org/abs/astro-ph/0212251 Rankin S., 1995, Black Holes
And Quantum Gravity,
http://www.damtp.cam.ac.uk/user/gr/public/bh_hawk.html Reynolds C.,
1997, Evidence For the Black Hole Model,
http://www.astro.umd.edu/~chris/thesis/node9.html
Reynolds S., Nowak M. A., 2003, Fluorescent Iron Lines As A Probe of
Astrophysical Black Hole Systems, http://www.astro.umd.edu/~chris/publications/html_papers/ironlines_plain/ironlines_pl
ain.html
Russell S., Halls B., 1999, Missing Matter (Swinburne University Of
Technology – Swinburne Astronomy Online HET603) Schombert J., 2002, Theory
Of Everything,
http://zebu.uoregon.edu/~js/21st_century_science/lectures/lec17.html
Seidel E., 1995, The Relativistic Universe,
http://archive.ncsa.uiuc.edu/Cyberia/NumRel/RelUniverse1.html Sekmen
S., 2003, Search For Higgs Boson In The Extra-Dimensional Black Hole Decays
At LHC,
http://www.physics.metu.edu.tr/he_seminars/files/1
Silber k., 1999, Weighting Black Holes The Easy Way,
http://www.space.com/scienceastronomy/astronomy/black_holes_measure.html
SDSS (Sloan Digital Sky Survey), 2002, The Power Source Of Quasars,
http://skyserver.sdss.org/dr1/en/proj/advanced/quasars/power.asp
Smarr L.., 1995, The Einstein Field Equations,
http://archive.ncsa.uiuc.edu/Cyberia/NumRel/EinsteinEquations.html
Smith G., 1999, Dark Matter In The Universe,
http://cassfos02.ucsd.edu/public/tutorial/DM.html
Thinkquest, 1999, Conceiving Black Holes,
http://library.thinkquest.org/25715/discovery/conceiving.htm
Thinkquest, 1999, Formation Of A Stellar Black Holes,
http://library.thinkquest.org/25715/formation/stellar.htm#chandrasekhar
Thinkquest, 2000, Hawking Radiation,
http://library.thinkquest.org/C007571/english/advance/english.htm
Thorne K. S., 1994, Black Holes & Time Warps
Thomas S., Giddings S. B., 2002, High Energy Colliders As Black Hole
Factories: The End Of Short Distance Physics,
http://www.arxiv.org/abs/hep-ph/0106219
Tucker W., 2000, Chandra Discovers X-Ray Source At The Centre Of Our
Galaxy,
http://chandra.harvard.edu/press/00_releases/press_011400gc.html
Visser M., Wiltshire D. L., 2004, Stable Gravastars – An Alternative To
Black Holes?,
http://www.iop.org/EJ/abstract/0264-9381/21/4/027
Watson M., 2001, Black Hole Observations,
http://www.pas.rochester.edu/~dmw/ast102/Lectures/Lect_16p.pdf Watzke
M., 2003, “Iron Clad” Evidence For Spinning Black Hole,
http://chandra.harvard.edu/press/03_releases/press_091703.html
Weinstock M., 2000, Scientists Pinpoint Milky Way Galaxy’s Black Hole,1
http://www.space.com/scienceastronomy/astronomy/our_black_hole_000920.html
Weiss M., 2004, Quasars And Active Galaxies,
http://chandra.harvard.edu/xray_sources/quasars.html
Weisstein E. W., 2004, Black Hole,
http://scienceworld.wolfram.com/physics/BlackHole.html Weisstein E.
W., 2004, Singularity Theorem,
http://scienceworld.wolfram.com/physics/SingularityTheorem.html
Weisstein E. W., 2004, Price’s Theorem,
http://scienceworld.wolfram.com/physics/PricesTheorem.html
Back to Top |
Back to
High Mass Stellar Evolution Image
Credits: Figure 2: NCSA – University of Illinois
Figure 3: NCSA – University of Illinois
Figure 4: NCSA – University of Illinois
Figure 5: NCSA – University of Illinois
Figure 6: NASA – Hubble Space Telescope Website
Figure 7: Haynes R. -NASA/CXC/SAO
Figure 8: NASA – Hubble Space Telescope Website
Figure 9: Mirabel I. F.
Figure 10: NASA/CXC/SAO
Figure 11: Sekmen S.
Back to Top |
Back to
High Mass Stellar Evolution
|

